3. Meshes in Monocurl
We'll now talk about meshes, the objects that we see on screen. This section is a bit long, but a lot of it is just examples. The optional sections discuss some of the decisions behind Monocurl, but are not that practical so feel free to skim them.
3.1 Following Along
In this section, you finally have many opportunities to follow along!
Simply create a new scene in the Monocurl editor, and in the slide_1 section, add the required code for creating the meshes.
We haven't officially discussed animations yet, but for now you'll have to use the following lines to show the meshes we create. You might also want to change the background to WHITE for some scenes with black meshes.
tree main = ...
p += Set:
vars&: main
A full working example looks something like this (try it out!). Remember that these lines should be present in the slide_1 section.
tree circ = Circle:
center: ORIGIN
radius: 1
tag: {}
color: default
p += Set:
/* replace circ with whatever variable contains the meshes */
vars&: circ
3.2 Background Knowledge
IMPORTANT The final prerequisite before we actually get to meshes is understanding the coordinate system.
Monocurl operates in a right handed coordinate system (so positive z faces away from the screen). Other than that, the following image gives a good glimpse at the default system. Thus, if you want to have a circle span left to right, its radius should be 4.
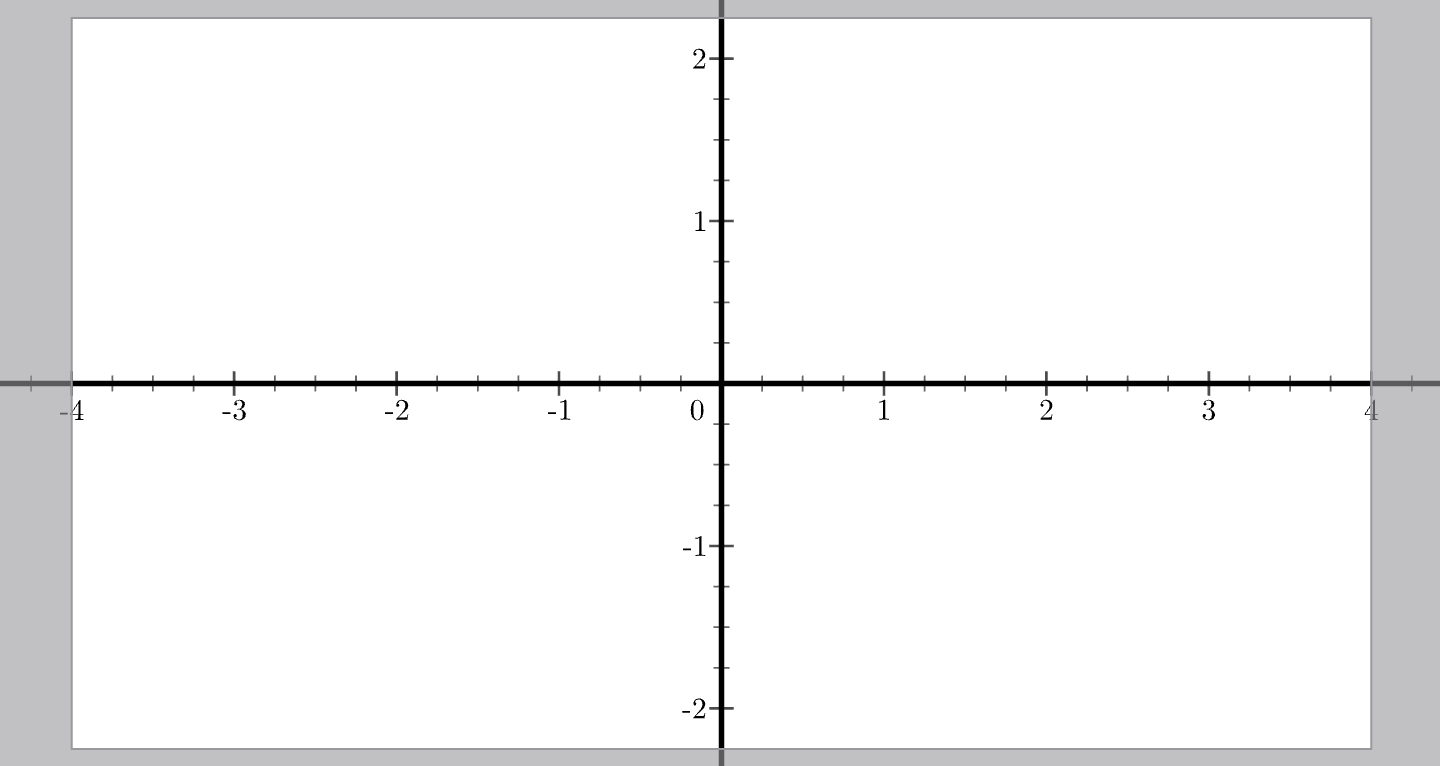
Also, whenever a function asks for a color, it means a vector of four numbers (red, green, blue, alpha), each in the range of 0 to 1. To actually change the color of most meshes, you'll likely have to click on the <> icons next to color (see functor modes from previous lesson).
3.3 Meshes
DEFINITION A mesh is a connected* collection of dots, lines, and triangles. Each vertex has an associated color.
Primitive meshes are meshes that you can create directly (i.e. no prerequisite meshes needed). Some common examples:

- Circle is a simple geometric circle
- Tex can be used to render latex equations
- ColorGrid displays a bunch of rectangles according to a user-provided color function
- Axis2d is helpful in graphing scenes
Operator meshes (or more accurately, operators on meshes) take in one or more mesh-trees, and spit out a new a mesh-tree. Here are a few examples (you can find more in the documentation section):
- Shifted translates a mesh-tree by a certain delta
- Rotated rotates a mesh-tree along a given axis
- Centered translates the mesh-tree so that its center is placed at the given location
- PointMapped moves every single vertex in the mesh-tree to a new point using the given transformation function
- XStack arranges a series of meshes in the x direction
3.4 Mesh-Tree
Typically, we want to consider not just a single mesh, but a collection of them. This is where mesh-trees come in.
DEFINITION A mesh-tree is defined recursively. A mesh is a mesh-tree. A vector of mesh-trees is a mesh-tree.
Informally, we can think of a mesh-tree as just a list of meshes, that might have similar such lists inside of them. Example (assuming all the variables are meshes): {mesh_a, mesh_b, {{{{mesh_c}}}}, {mesh_d, {mesh_e}}}.
REMARK To those who ask why we can't just use a flat vector, note that mesh-trees allow us to be sloppy with the structure of our variables, which makes programming much easier. It also provides some sort of abstraction where we can ignore the exact details of how functions structure their returned mesh-trees. For instance, notice the following simple example where the baloons vector is not a flat list:
func Balloon(position) = identity:
let head = Circle:
center: position
radius: 0.5
tag: {}
stroke: BLACK
let string = Line:
start: head
end: vec_sub(position, {0, 2, 0})
tag: {}
stroke: BLACK
element: {head, string}
tree balloons = {}
balloons += Balloon:
position: {-1, 0, 0}
balloons += Balloon:
position: {1, 0, 0}
/* at this point balloons has the following structure: */
/* {{head_1, string_1}, {head_2, string_2}} */
p += Set:
vars&: balloons
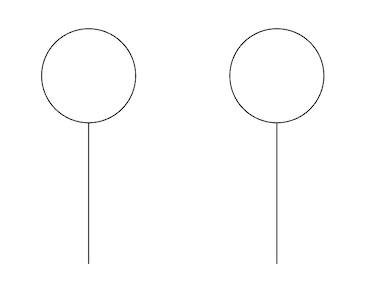
IMPORTANT Most library functions dealing with meshes allow you to input an entire mesh-tree. Operations on a mesh-tree simply operate on all the meshes contained within the tree.
3.5 (Optional) Why meshes?
In many computer graphics contexts, Bezier curves are used instead of the meshes we just talked about. The decision to use meshes primarily comes as a way to make all screen objects the same type, which is harder to do with Bezier curves. On the other hand, there are instances where meshes are much less smooth than Bezier curves, which is undesirable.
For instance, the following would require many Bezier curve objects, but can be done in a single mesh.

3.6 Complex Example
To create complex scenes, you have to think about the constiuent parts, and how each own can be written as a pipeline of primitives and operators. Here's an example and the result:

Code:
/* helper function, takes in number of lines and radius */
func Cardiod(n, r) = identity:
var ret = {}
ret += Circle:
center: ORIGIN
radius: r
tag: {}
stroke: LIGHT_GRAY
func theta_to_point(theta) = {r * cos(theta), r * sin(theta), 0}
for i in 0 :< n
let next = mod(i * 2, n)
let org_theta = TAU * i / n
let new_theta = TAU * next / n
ret += Line:
start: theta_to_point(org_theta)
end: theta_to_point(new_theta)
tag: {}
stroke: BLACK
element: ret
/* create 9 raw cardiods */
let raw_cards = map:
v: 1 :< 10
f(x): Cardiod:
n: 2 * x + 1
r: 0.25
/* use operators to position them */
tree cards = Centered:
/* for simple operators it can be okay to use functions */
mesh: XStack(raw_cards)
at: ORIGIN
p += Set:
vars&: cards
3.7 More Examples!
Here's the code for a Koch Curve and the result:
func move(start, mag, rotation) = identity:
let delta = {mag * cos(rotation), mag * sin(rotation), 0}
element: vec_add(start, delta)
func KochCurve(level, start, length, rotation) = identity:
var ret = {}
if level > 0
var pos = start
var rot = rotation
ret += KochCurve:
level: level - 1
start: pos
length: length / 3
rotation: rot
pos = move(pos, length / 3, rot)
rot += PI / 3
ret += KochCurve:
level: level - 1
start: pos
length: length / 3
rotation: rot
pos = move(pos, length / 3, rot)
rot += 4 * PI / 3
ret += KochCurve:
level: level - 1
start: pos
length: length / 3
rotation: rot
pos = move(pos, length / 3, rot)
rot += PI / 3
ret += KochCurve:
level: level - 1
start: pos
length: length / 3
rotation: rot
else
ret += Line:
start: start
end: move(start, length, rotation)
tag: {}
stroke: BLACK
element: ret
let l = 4
tree k = KochCurve:
level: 5
start: {-l / 2, 0, 0}
length: l
rotation: 0
p += Set:
vars&: k
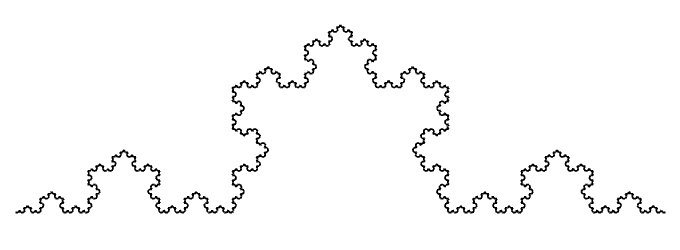
Here's one for the difference between two functions
func f(x) = sin(x) ** 2
func g(x) = sin(x) * 4 / 5
tree scene = {}
scene += Axis2d:
center: ORIGIN
x_unit: 2
x_rad: 4
x_label: "x"
y_unit: 1
y_rad: 1.5
y_label: "y"
grid: off
tag: {}
color: BLACK
var graphs = {}
graphs += ExplicitFunc:
start: -4
stop: 4
f(x): f(x)
tag: {}
stroke: RED
graphs += ExplicitFunc:
start: -4
stop: 4
f(x): g(x)
tag: {}
stroke: BLUE
graphs += ExplicitFuncDiff:
start: -4
stop: 4
f(x): f(x)
g(x): g(x)
tag: {}
pos_fill: {1,0,0,0.2}
neg_fill: {0,0,1,0.2}
/* helps morph meshes into the axis space */
scene += EmbedInSpace:
mesh: graphs
axis_center: ORIGIN
x_unit: 2
y_unit: 1
z_unit: 1
p += Set:
vars&: scene
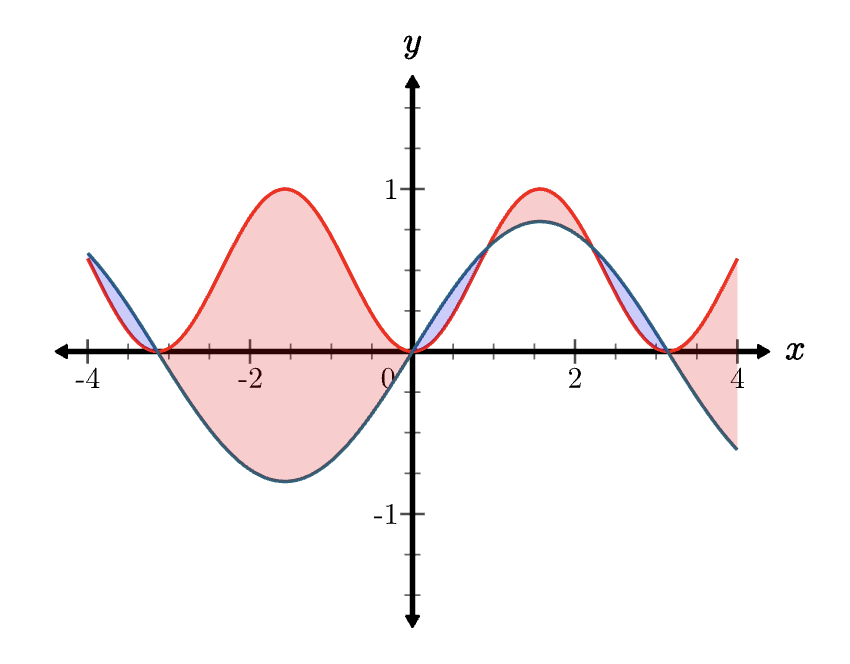
Riemann rectangles
func LRAM(start, stop, n, q(x)) = identity:
var ret = {}
let delta = (stop - start) / n
for i in 0 :< n
let x_start = start + delta * i
let x_end = x_start + delta
let val = q(x_start)
ret += Rect:
center: {(x_start + x_end) / 2, val / 2, 0}
width: delta
height: val
tag: {}
stroke: BLACK
fill: {1,1,0,0.2}
element: ret
func q(x) = x * x
tree scene = {}
scene += Axis2d:
center: {-1.5,-1.5,0}
x_unit: 1
x_min: 0
x_max: 3
x_label: "x"
y_unit: 3
y_min: 0
y_max: 9
y_label: "y"
grid: off
tag: {}
color: BLACK
var graphs = {}
graphs += ExplicitFunc:
start: 0
stop: 3
f(x): q(x)
tag: {}
stroke: RED
graphs += LRAM:
start: 0
stop: 3
n: 6
q(x): q(x)
scene += EmbedInSpace:
mesh: graphs
axis_center: scene[0].center
x_unit: 1
y_unit: 3
z_unit: 1
p += Set:
vars&: scene
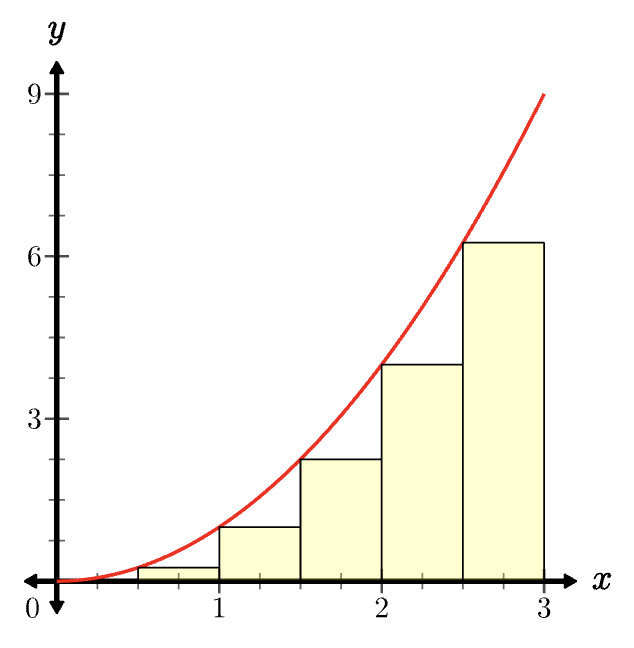
The color grid from before
tree grid = ColorGrid:
x_min: 0
x_max: 1
y_min: 0
y_max: 1
x_step: 0.2
y_step: 0.2
tag: {}
color_at(pos): {pos[0], pos[1], 1, 1}
stroke: BLACK
p += Set:
vars&: grid

Some famous LaTeX equations
tree equations = Text:
var str = "\begin{align*}"
str += "\int_{-\infty}^{\infty}e^{-x^2}dx &= \sqrt{\pi} \\"
str += "e^{\pi i} + 1 &= 0 \\"
str += "x &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \\"
str += "\end{align*}"
text: str
scale: 0.75
stroke: CLEAR
fill: BLACK
equations = Centered:
mesh: equations
at: ORIGIN
p += Set:
vars&: equations
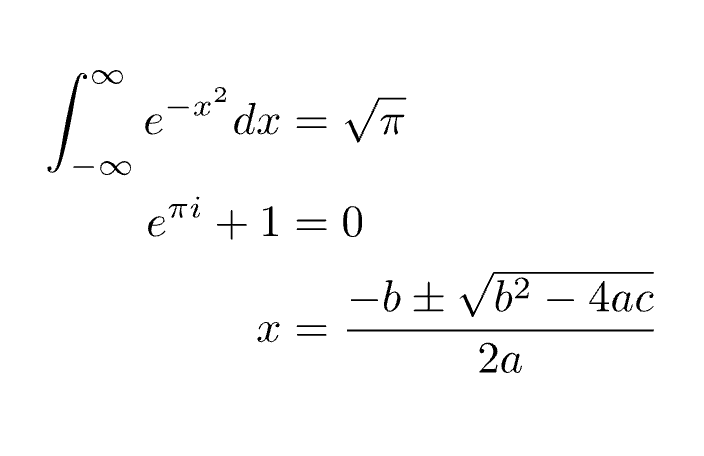
Torus (with some camera work)
/* checkerboard */
let uv_base = ColorGrid:
x_min: 0
x_max: 1
y_min: 0
y_max: 1
x_step: 0.05
y_step: 0.05
tag: {}
color_at(pos): identity:
let r = round(pos[0] / 0.05)
let c = round(pos[1] / 0.05)
var col = BLACK
if mod(r + c, 2)
col = RED
element: col
let r1 = 1
let r2 = 0.5
tree torus = PointMapped:
mesh: uv_base
point_map(point): identity:
let u = point[0] * TAU
let v = point[1] * TAU
let x = (r1 + r2 * cos(v)) * cos(u)
let y = (r1 + r2 * cos(v)) * sin(u)
let z = r2 * sin(v)
element: {x,y,z}
p += Set:
vars&: torus

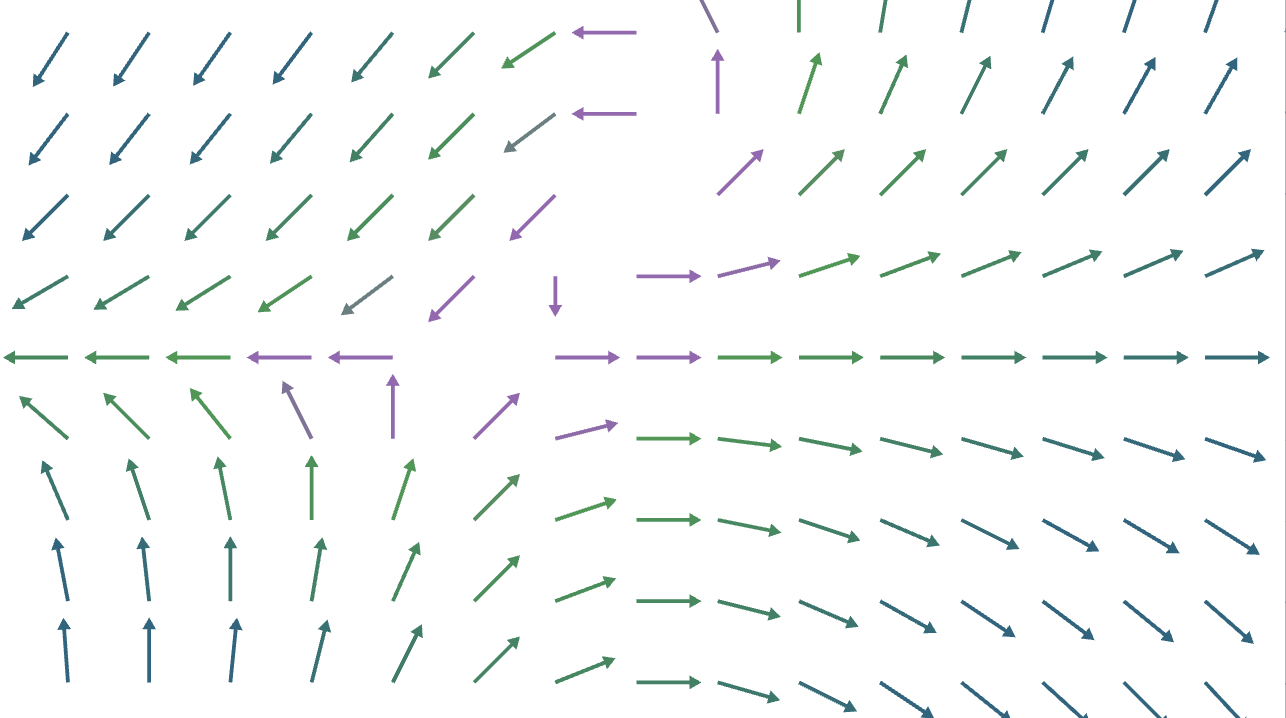
Vector Field
/* somewhat hard coded for sake of example */
let min_norm = 1
let max_norm = 5
let max_scaled_norm = 0.4
var gradient = {:}
gradient[min_norm] = PURPLE
gradient[1.5] = GREEN
gradient[max_norm] = BLUE
let gradient_c = gradient
func VectorField(f(x,y)) = Field:
x_min: -4
x_max: 4
y_min: -2
y_max: 2
mesh_at(pos): Vector:
var raw_delta = f(pos[0], pos[1]) + 0
let mag = norm(raw_delta)
let color = keyframe_lerp(gradient_c, mag)
var scale = 1
if mag > max_scaled_norm
scale = max_scaled_norm / mag
raw_delta = vec_mul(scale, raw_delta)
tail: pos
delta: raw_delta
tag: {}
stroke: CLEAR
fill: color
tree field = VectorField:
f(x, y): {-y+x+1,x*y}
p += Set:
vars&: field
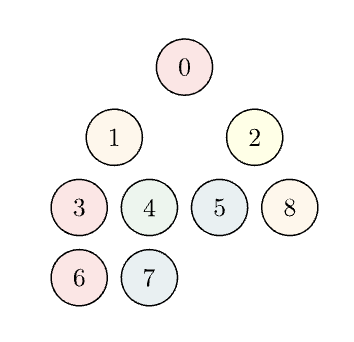
Tree (Graph Theory)
func tint(color) = {color[0], color[1], color[2], 0.1}
func Node(position, color, label) = identity:
var ret = {}
ret += Circle:
center: position
radius: 0.2
tag: {}
stroke: BLACK
fill: tint(color)
ret += Number:
value: label
precision: 0
scale: 0.5
tag: {}
stroke: CLEAR
fill: BLACK
ret[1] = Centered:
mesh: ret[1]
at: position
element: ret
/* we can add edges as well using a technique in lesson 7 */
/* without that, they are hard to add unfortunately */
func Tree(adj, colors, curr, position) = identity:
var ret = {}
ret += Node:
position: position
color: colors[curr]
label: curr
var children = {}
for child in adj[curr]
children += Tree(adj, colors, child, position)
/* position */
children = XStack:
mesh_vector: children
align_dir: UP
ret += children
ret = Stack:
mesh_vector: ret
dir: DOWN
align: center
element: ret
/* adjacency list */
let adj = {{1,2}, {3, 4}, {5, 8}, {6}, {7}, {}, {}, {}, {}}
let colors = {RED, ORANGE, YELLOW, RED, GREEN, BLUE, RED, BLUE, ORANGE}
tree graph = Tree:
adj: adj
colors: colors
/* 0 is root */
curr: 0
position: {0,1,0}
p += Set:
vars&: graph
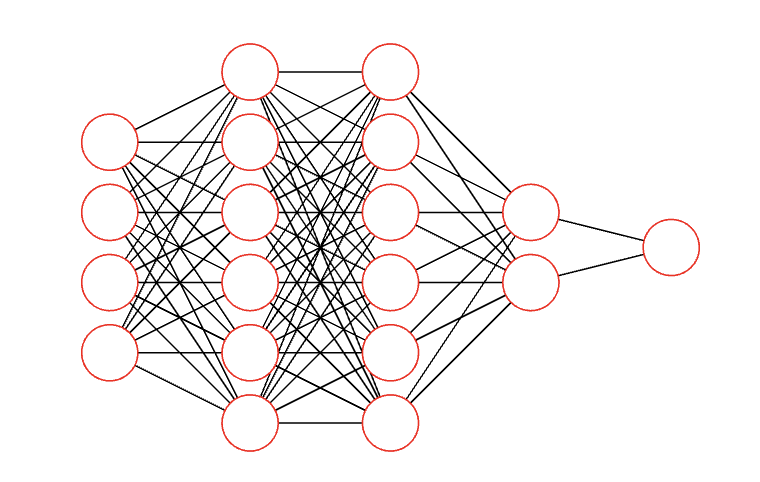
Neural Network
func NeuralNetwork(layer_counts) = identity:
var layers = {}
var edges = {}
var last_layer = {}
for i in 0 :< len(layer_counts)
var new_layer = {}
for j in 0 :< layer_counts[i]
new_layer += Circle:
center: {0, 0, 0}
radius: 0.2
tag: {}
stroke: RED
fill: WHITE
new_layer = YStack(new_layer)
new_layer = Centered:
mesh: new_layer
at: {i, 0, 0}
layers += new_layer
for prev in last_layer
for curr in new_layer
edges += Line:
start: prev
end: curr
tag: {}
stroke: BLACK
last_layer = new_layer
element: Centered:
mesh: {edges, layers}
at: ORIGIN
tree nn = NeuralNetwork:
layer_counts: {4, 6, 6, 2, 1}
p += Set:
vars&: nn
Look at more examples over here
3.8 Practice
Finally, you can try playing around with Monocurl! We still can't do animations yet, but as a challenge, try creating the following:
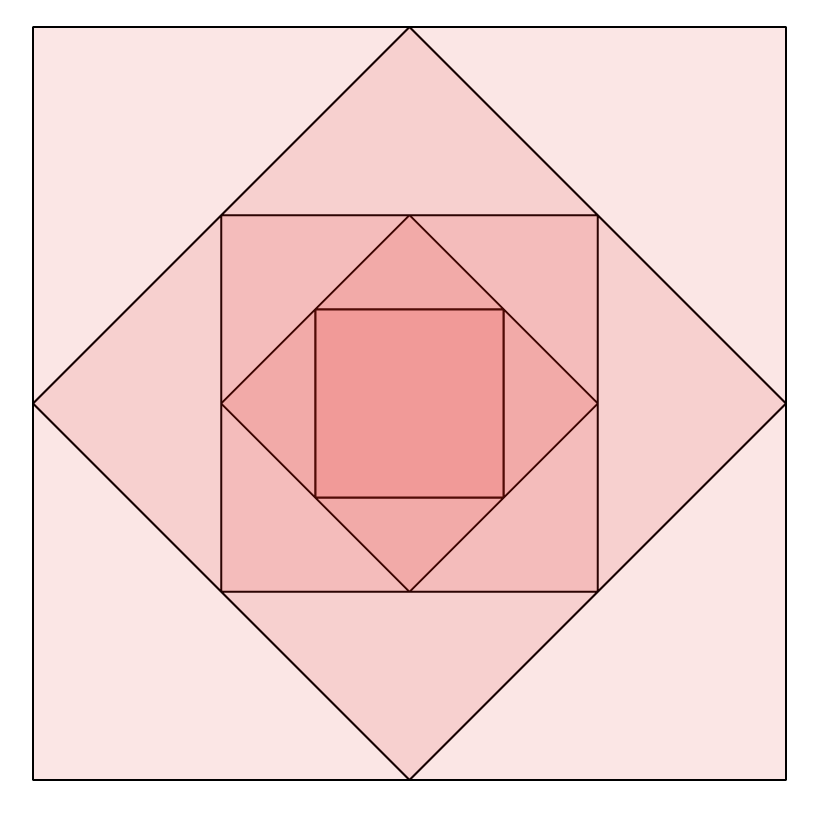
Hint, you can make the previous using just the following three meshes and operators (and a bit of math):
First get the placements right, then aim for the colors.
3.9 Conclusion
REMARK This sections covered the basics of meshes. The point isn't that you know all meshes by now, but rather you have a good enough idea that it's easy to learn new ones. We definitely recommend going to the docs page and exploring existing options. In particular, look out for the ones with a star, as those are pretty useful.
Also, hopefully you can see the importance of creating your own functions from the very few examples we gave. As scenes get more complex, functions are of even more importance.
3.10 (Optional) Remarks
REMARK I dont really like positioning (and think it gets pretty redundant), and there are some stuff to be improved. But overall, I think meshes are good enough for the beta release.